Guia de Funcionamento dos Métodos
Nesta seção será demonstrada, a partir de exemplos, o funcionamento dos métodos disponíveis nesta página. Siga corretamente as instruções para chegar aos resultados esperados. Para utilizar os métodos, observe a figura abaixo:

Após selecionada a opção desejada, dê um clique na mesma para que o método escolhido apareça no centro da página.

O funcionamento de cada um dos métodos será explicado posteriormente.
Funções
As funções são especificadas através de operações matemáticas e funções pré-definidas, onde estas últimas são utilizadas por meio do modo de chamada. Quaisquer combinação das anteriores também será válida seguindo os padrões de expressões matemática. As operações matemáticas podem ser feitas usando os operadores +, -, *, / e ^. Vale observar a prioridade de uma operação em relação a outra. As operações de * e / têm a mesma prioridade juntas e realizadas primeiro em relação as operações de + e -, onde estas últimas têm a mesma prioridade. Pode-se utilizar parênteses para mudar a precedência da expressão. As partes fracionárias de números reais são consideradas após o uso do "." (exemplo: 3.1415). Os cálculos são realizados da esquerda para direita. Cada um dos operadores será descrito abaixo:
- Operador +
Este operador é utilizado para efetuar operações de adição entre dois ou mais operandos. Exemplo: 2+2+(5+1).
- Operador -
É o operador usado para realizar operações de subtração entre dois ou mais operandos. Exemplo: 1+4-5+(-3).
- Operador *
A multiplicação entre dois ou mais operandos é feita através deste operador. Exemplo: 5*(-7).
- Operador /
O operador / faz a divisão entre dois ou mais operandos. Não realizará a operação caso o denominador seja 0. Exemplo: 2/(3*4.49).
- Operador ^
Este operador realiza o cálculo de um número elevado a outro. Exemplo: 5^4.
Funções Pré-Definidas
Alguns métodos necessitam de funções para que sejam efetuados os cálculos para a obtenção do(s) resultado(s) desejado(s). Assim, é necessário indicar qual a função que será utilizada. A seguir, segue a lista dos nomes das funções que podem ser usadas para definir outras funções.
- Função sqr
Modo de chamada: sqr( ).
Descrição: retorna o quadrado do argumento (parâmetro) especificado.
Exemplo de chamada: sqr(2.456)
- Função sqrt
Modo de chamada: sqrt( ).
Descrição: retorna a raiz quadrada do argumento (parâmetro) especificado.
Exemplo de chamada: sqrt(2.25)
- Função abs
Modo de chamada: abs( ).
Descrição: retorna o valor absoluto do argumento (parâmetro) especificado.
Exemplo de chamada: abs(-1)
- Função ln
Modo de chamada: ln( ).
Descrição: retorna o logaritmo de base neperiana do argumento (parâmetro) especificado.
Exemplo de chamada: ln(2.7)
- Função log
Modo de chamada: log( ).
Descrição: retorna o logaritmo de base 10 do argumento (parâmetro) especificado.
Exemplo de chamada: log(1)
- Função exp
Modo de chamada: exp( ).
Descrição: retorna o valor do número de Euller (2.718281828459045) elevado ao argumento (parâmetro) especificado.
Exemplo de chamada: exp(1)
- Função sen
Modo de chamada: sen( ).
Descrição: retorna o seno do argumento (parâmetro), em radianos, especificado .
Exemplo de chamada: sen(3.1415)
- Função cos
Modo de chamada: cos( ).
Descrição: retorna o cosseno do argumento (parâmetro), em radianos, especificado.
Exemplo de chamada: cos(2*3.14)
- Função tan
Modo de chamada: tan( ).
Descrição: retorna a tangente do argumento (parâmetro), em radianos, especificado.
Exemplo de chamada: tan(3.1415/4)
- Função csc
Modo de chamada: csc( ).
Descrição: retorna a cossecante do argumento (parâmetro), em radianos, especificado.
Exemplo de chamada: csc(3.14)
- Função sec
Modo de chamada: sec( ).
Descrição: retorna a secante do argumento (parâmetro), em radianos, especificado.
Exemplo de chamada: sec(0)
- Função cotan
Modo de chamada: cotan( ).
Descrição: retorna a cotangente do argumento (parâmetro), em radianos, especificado.
Exemplo de chamada: cotan(3.141592653589793/4)
- Função senh
Modo de chamada: senh( ).
Descrição: retorna o seno hiperbólico do argumento (parâmetro) especificado.
Exemplo de chamada: senh(1)
- Função cosh
Modo de chamada: cosh( ).
Descrição: retorna o cosseno hiperbólico do argumento (parâmetro) especificado.
Exemplo de chamada: cosh(2)
- Função tanh
Modo de chamada: tanh( ).
Descrição: retorna a tangente hiperbólica do argumento (parâmetro) especificado.
Exemplo de chamada: tanh(2)
OBS: a mensagem "NaN" (Not A Number) é exibida no resultado de algum cálculo quando o argumento passado para alguma função não é um número.
Sistemas Lineares
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente aos métodos de resolução de sistemas lineares:
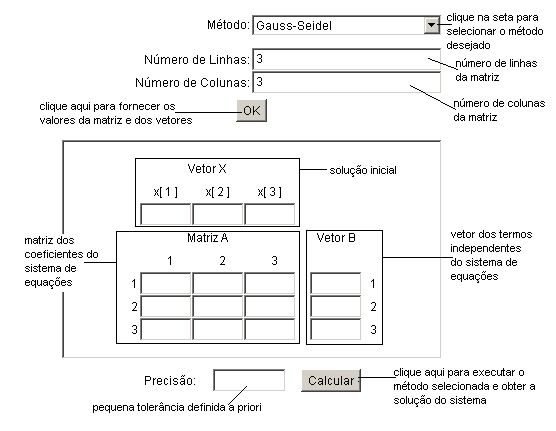
- Método: local onde será selecionado o método desejado para resolução do sistema linear;
- Número de Linhas: indica a quantidade de linhas da matriz;
- Número de Colunas: indica a quantidade de colunas da matriz;
- Matriz A: matriz que contém os coeficientes das equações;
- Vetor B: vetor que contém os coeficientes dos termos independentes;
- Vetor X: vetor que contém a solução inicial do sistema.
Sistemas Não-Lineares
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente aos métodos de resolução de sistemas não-lineares:
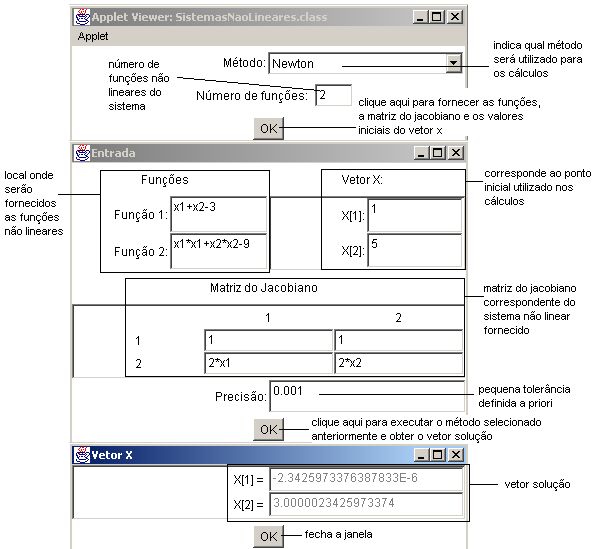
- Método: local onde será selecionado o método desejado para resolução do sistema linear;
- Número de funções: indica a quantidade de funções do sistema;
- Funções: local onde serão digitadas as funções;
- Vetor X: corresponde aos valores iniciais deste vetor;
- Matriz do Jacobiano: contém os coeficientes da matriz do jacobiano;
- Precisão: pequena tolerância positiva definida a priori.
Interpolação Polinomial
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente aos métodos de Interpolação Polinomial:
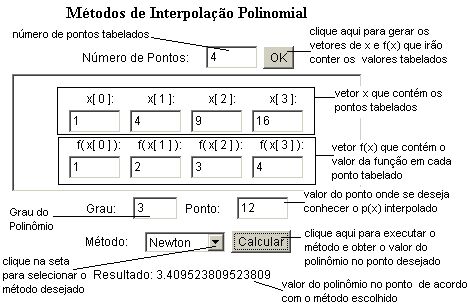
Método Simplex Revisado
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente ao Método Simplex:
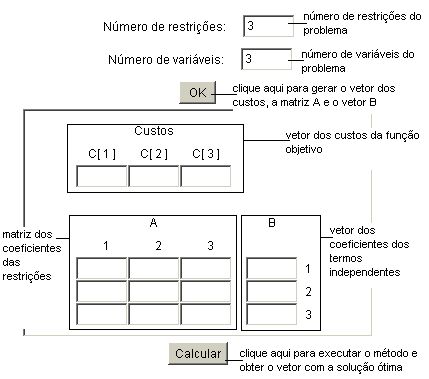
Zero de Funções
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente aos métodos de zero de funções:

- Função: local onde será inserida a função que será utilizada no método escolhido;
- Métodos: indica qual método será escolhido para efetuar os cálculos;
- Ponto Inicial: corresponde ao ponto inicial do intervalo, que contém a raiz, utilizado no método;
- Ponto Final: corresponde ao ponto final do intervalo, que contém a raiz, utilizado no método;
- Precisão: pequena tolerância positiva definida a priori;
- X0: ponto inicial (pertence ao intervalo dado).
Integração Numérica
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente aos métodos de integração numérica:

- Digitar função: se selecionada, possibilita o usuário entrar com a função desejada;
- Valores tabelados: se selecionada, abrirá uma opção onde o usuário deve fornecer o número de valores tabelados e, em seguida, clicar no botão "OK" para abrir uma janela onde deverão ser fornecidos estes valores ( se o método escolhido for 1/3 de Simpson, o número de valores tabelados deve ser par; se o método escolhido for 3/8 de Simpson, deve ser ímpar);
- Função: local onde será inserida a função que será utilizada no método escolhido;
- Número de valores tabelados: indica a quantidade de valores fornecidos pelo usuário para calcular a integral;
- Valor aproximado da integral: resultado aproximado da integral;
- Ponto inicial: corresponde ao ponto inicial do intervalo onde será calculada a integral;
- Ponto final: refere-se ao ponto final do intervalo onde será calculada a integral;
- Número de Pontos: número de pontos do intervalo;
- 1/3 de Simpson: indica o método de 1/3 de Simpson para calcular a integral;
- 3/8 de Simpson: indica o método de 3/8 de Simpson para calcular a integral;
- Trapézios: indica o método dos Trapézios para calcular a integral.
Equações Diferenciais
(clique no título para consulta de teoria sobre os métodos)
(clique aqui para consulta dos algoritmos sobre os métodos)
Observe a figura abaixo correspondente aos métodos de Equações Diferenciais:

- Y': EDO de ordem 1;
- X0: valor inicial do P.V.I.;
- Y0: valor inicial do P.V.I.;
- Xn: extremo direito do intervalo;
- Número de pontos: número de pontos do intervalo (será usado para cálculo do passo se não estiver da cor cinza, onde esta cor representa opção desabilitada);
- h: valor do passo (será usado para cálculo do número de pontos se não estiver da cor cinza, onde esta cor representa opção desabilitada);
- Euller indica o método de Euller para calcular os aproximantes;
- Euller Modificado indica o método de Euller Modificado para calcular os aproximantes;
- Runge-Kutta de Ordem 4 indica o método de Runge-Kutta de Ordem 4 para calcular os aproximantes;
- Resultado: valor do último aproximante calculado.









